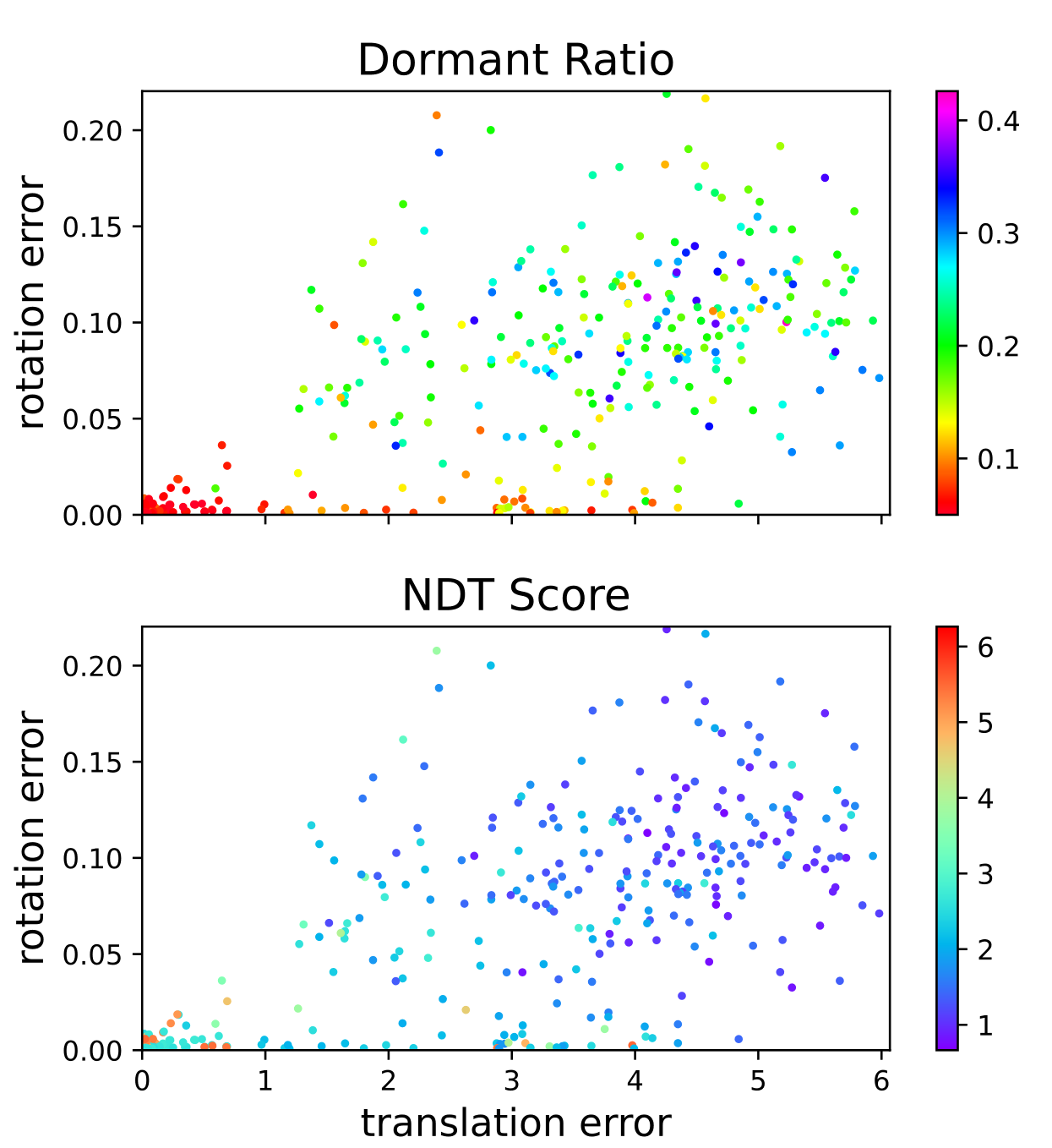
Dormant Ratio Certification
A Novel Certification for Optimization-based Registrations

Affiliation: ITRI
Advised by Chieh-Chih (Bob) Wang, Ph.D.
Dormant Point refers to source points not contributing to the optimization. In particular, we analyze the pointwise contribution from the following aspects:
- NDT scores
- Local Jacobian smoothness
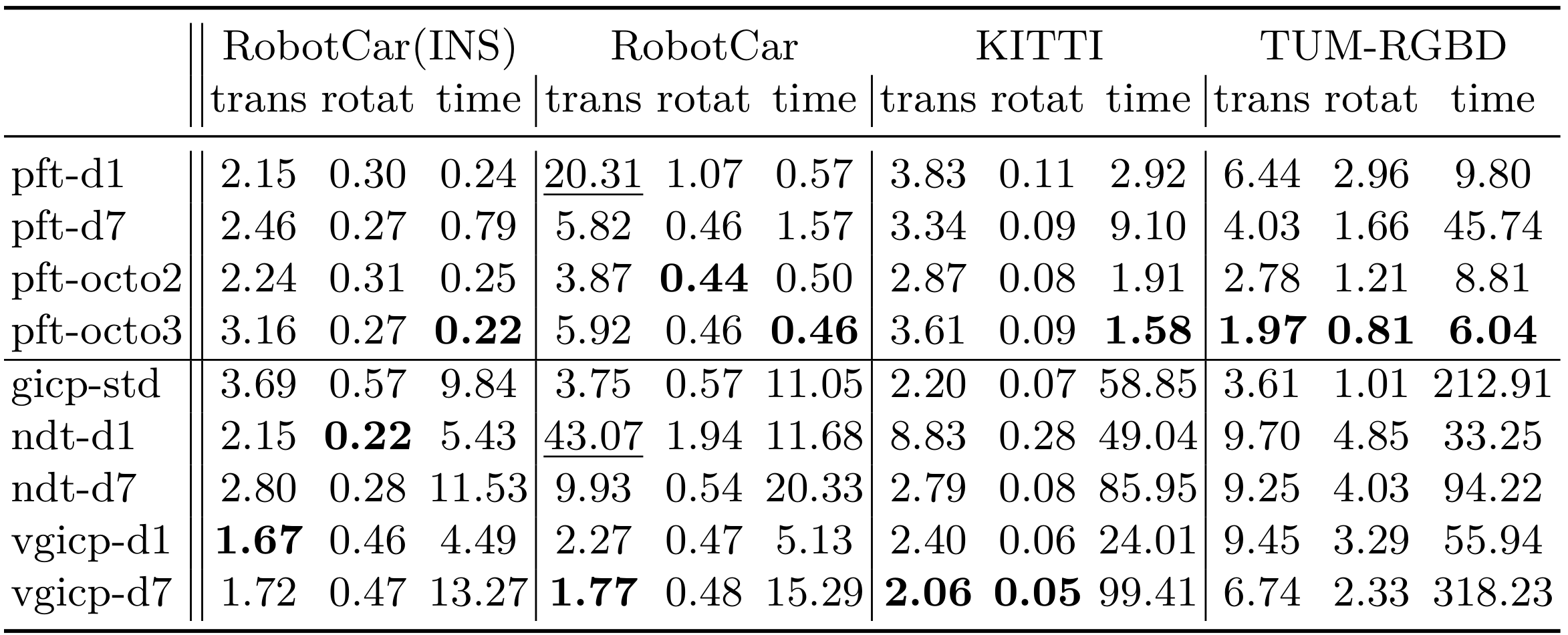
As a result, our new metric remains precise and consistent over environmental and parameter changes.